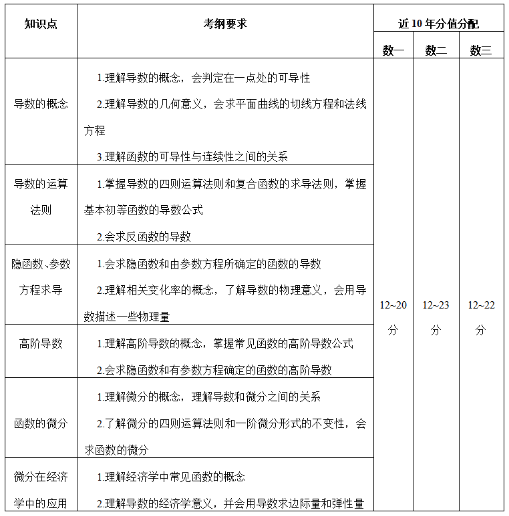
一、一元函數微分學
本章節重點有導數的概念與計算,其中復合函數求導、參數方程求導都是每年的常考點,同學們要多做題、多練習,還有微分中值定理是高等數學中一大難點和重點,輔助函數的構造以及變形需要重點理解并掌握。另外,要學會利用導數判斷函數的性態,例如函數的單調性、函數取得極值的第一、第二充分條件 、凹凸性判斷的以及曲線漸近線的計算。因此,我們在學習的時候要重視基礎,對導數定義及基本導數公式、麥克勞林公式要熟練背誦,在此基礎上靈活運用微分中值定理,判斷函數的性態。
二、一元函數積分學
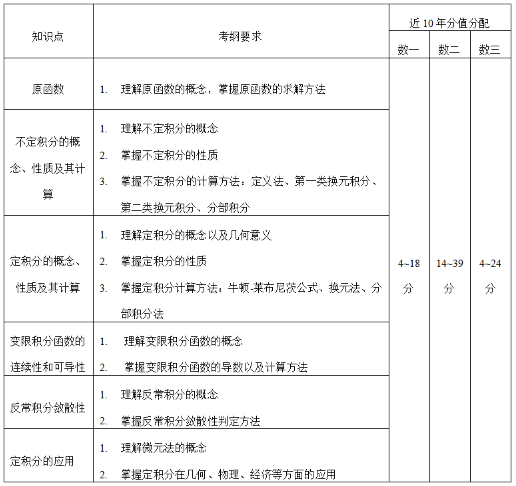
本章節重點是要學會不定積分和定積分的計算,熟練背誦基本積分表,在此基礎上,要會用學會第一類和第二類換元積分法,第一類換元法主要是湊微分法,第二類換元法主要用變量代換,包含三角函數代換、倒代換、無理式代換等,還要學會分部積分法,能運用合適的方法計算不定積分。定積分主要理解其定義及積分上限函數的性質與求導,此部分內容綜合性較強,常與極限、級數以及微分方程綜合考查,所以同學們要多花時間,總結常考題型,多練習,做到有的放矢。
三、多元函數微分學
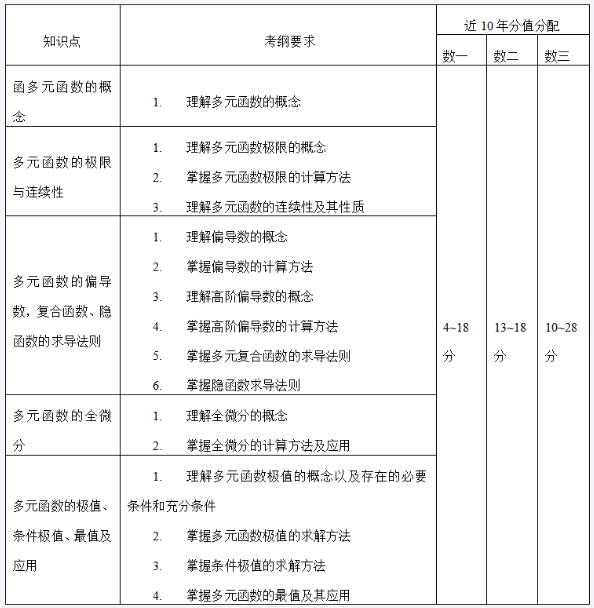
多元函數微分學主要考二元或三元函數的微分與偏導數以及高階偏導數寫得求法,要正確理解多元函數連續、偏導與可微的關系,這是歷年的必考點。要掌握求多元函數高階偏導數的邏輯規律,包括復合函數的偏導以及隱函數求偏導,對于復合函數求偏導首先要確定自變量與應變量,根據全微分公式以及鏈式法則依次求偏導,對于隱函數要會求又一個方程確定的隱函數及由方程組確定的隱函數求偏導。另外,本章還要求我們掌握多元函數的極值和條件極值,要熟記二元函數極值存在的充分條件,會利用拉格朗日常數法求條件極值。
四、二重積分
多元函數積分學內容多,計算量大。主要包含二重積分和三重積分、曲線曲面積分。其中數二、三的同學僅需要掌握二重積分就好。此處重點掌握二重積分在直角坐標和極坐標下的計算,并能夠根據積分區域的特點靈活轉換坐標系,會運用被積函數的奇偶性及積分區域的對稱性化簡二重積分,根據被積函數或積分區域選擇適當的坐標系進行計算。
對于數一的同學來說,除了要掌握二重積分,還要掌握三重積分的計算(直角坐標、柱面坐標、球面坐標),第一類曲線積分和第二類曲線積分的計算,第一類曲面積分和第二類曲面積分的計算,對曲線曲面積分的計算要熟記計算公式,不同的曲線(面)扥性質,會應用積分區域和被積函數化簡計算過程。這部分內容理解比較困難,要根據真題總結計算規律,每一類計算做到心中有數。
本文素材來源于網絡,由武漢新文道考研進行整理,想了解更多關于考研相關資訊,敬請關注新文道考研,我們將為同學們奉上全面完整的時下考研相關資訊。













 關注武漢新文道微信
關注武漢新文道微信